In part 1 of this 2-part series, I introduced the notion of sensitivity to unmeasured confounding in the context of an observational data analysis. I argued that an estimate of an association between an observed exposure and outcome is sensitive to unmeasured confounding if we can conceive of a reasonable alternative data generating process (DGP) that includes some unmeasured confounder that will generate the same observed distribution the observed data. I further argued that reasonableness can be quantified or parameterized by the two correlation coefficients and , which measure the strength of the relationship of the unmeasured confounder with each of the observed measures. Alternative DGPs that are characterized by high correlation coefficients can be viewed as less realistic, and the observed data could be considered less sensitive to unmeasured confounding. On the other hand, DGPs characterized by lower correlation coefficients would be considered more sensitive.
I need to pause here for a moment to point out that something similar has been described much more thoroughly by a group at NYU’s PRIISM (see Carnegie, Harada & Hill and Dorie et al). In fact, this group of researchers has actually created an R package called treatSens to facilitate sensitivity analysis. I believe the discussion in these posts here is consistent with the PRIISM methodology, except treatSens is far more flexible (e.g. it can handle binary exposures) and provides more informative output than what I am describing. I am hoping that the examples and derivation of an equivalent DGP that I show here provide some additional insight into what sensitivity means.
I’ve been wrestling with these issues for a while, but the ideas for the derivation of an alternative DGP were actually motivated by this recent note by Fei Wan on an unrelated topic. (Wan shows how a valid instrumental variable may appear to violate a key assumption even though it does not.) The key element of Wan’s argument for my purposes is how the coefficient estimates of an observed model relate to the coefficients of an alternative (possibly true) data generation process/model.
OK - now we are ready to walk through the derivation of alternative DGPs for an observed data set.
Two DGPs, same data
Recall from Part 1 that we have an observed data model
where . We are wondering if there is another DGP that could have generated the data that we have actually observed:
where is some unmeasured confounder, and and . Can we go even further and find an alternative DGP where has no direct effect on at all?
(and ) derived from
In a simple linear regression model with a single predictor, the coefficient can be specified directly in terms , the correlation between and :
We can estimate from the observed data set, and we can reasonably assume that (since we could always normalize the original measurement of ). Finally, we can specify a range of (I am keeping everything positive here for simplicity), such that (where I assume a correlation of is at or beyond the realm of reasonableness). By plugging these three parameters into the formula, we can generate a range of ’s.
Furthermore, we can derive an estimate of the variance for ( ) at each level of :
So, for each value of that we generated, there is a corresponding pair .
Determine
In the addendum I go through a bit of an elaborate derivation of , the coefficient of in the alternative outcome model. Here is the bottom line:
In the equation, we have and , which are both estimated from the observed data and the pair of derived parameters and based on . , the coefficient of in the outcome model is a free parameter, set externally. That is, we can choose to evaluate all ’s the are generated when . More generally, we can set , where . (We could go negative if we want, though I won’t do that here.) If , and ; we end up with the original model with no confounding.
So, once we specify and , we get the corresponding triplet .
Determine
In this last step, we can identify the correlation of and , , that is associated with all the observed, specified, and derived parameters up until this point. We start by writing the alternative outcome model, and then replace with the alternative exposure model, and do some algebraic manipulation to end up with a re-parameterized alternative outcome model that has a single predictor:
where , , and .
As before, the coefficient in a simple linear regression model with a single predictor is related to the correlation of the two variables as follows:
Since ,
Determine
In order to simulate data from the alternative DGPs, we need to derive the variation for the noise of the alternative model. That is, we need an estimate of .
So,
where is the variation of from the observed data. Now we are ready to implement this in R.
Implementing in R
If we have an observed data set with observed and , and some target determined by , we can calculate/generate all the quantities that we just derived.
Before getting to the function, I want to make a brief point about what we do if we have other measured confounders. We can essentially eliminate measured confounders by regressing the exposure on the confounders and conducting the entire sensitivity analysis with the residual exposure measurements derived from this initial regression model. I won’t be doing this here, but if anyone wants to see an example of this, let me know, and I can do a short post.
OK - here is the function, which essentially follows the path of the derivation above:
altDGP <- function(dd, p) {
# Create values of rhoUD
dp <- data.table(p = p, rhoUD = seq(0.0, 0.9, length = 1000))
# Parameters estimated from data
dp[, `:=`(sdD = sd(dd$D), s2D = var(dd$D), sdY = sd(dd$Y))]
dp[, k1:= coef(lm(Y ~ D, data = dd))[2]]
# Generate b1 based on p
dp[, b1 := p * k1]
# Determine a1
dp[, a1 := rhoUD * sdD ]
# Determine s2ed
dp[, s2ed := s2D - (a1^2)]
# Determine b2
dp[, g:= s2ed/s2D]
dp <- dp[g != 1]
dp[, b2 := (a1 / (1 - g) ) * ( k1 - b1 )]
# Determine rhoUY
dp[, rhoUY := ( (b1 * a1) + b2 ) / sdY ]
# Eliminate impossible correlations
dp <- dp[rhoUY > 0 & rhoUY <= .9]
# Determine s2eyx
dp[, s2eyx := sdY^2 - (b1^2 * s2D + b2^2 + 2 * b1 * b2 * rhoUD * sdD)]
dp <- dp[s2eyx > 0]
# Determine standard deviations
dp[, sdeyx := sqrt(s2eyx)]
dp[, sdedx := sqrt(s2ed)]
# Finished
dp[]
}Assessing sensitivity
If we generate the same data set we started out with last post, we can use the function to assess the sensitivity of this association.
defO <- defData(varname = "D", formula = 0, variance = 1)
defO <- defData(defO, varname = "Y", formula = "1.5 * D", variance = 25)
set.seed(20181201)
dtO <- genData(1200, defO)In this first example, I am looking for the DGP with , which is implemented as in the call to function altDGP. Each row of output represents an alternative set of parameters that will result in a DGP with .
dp <- altDGP(dtO, p = 0)
dp[, .(rhoUD, rhoUY, k1, b1, a1, s2ed, b2, s2eyx)]## rhoUD rhoUY k1 b1 a1 s2ed b2 s2eyx
## 1: 0.295 0.898 1.41 0 0.294 0.904 4.74 5.36
## 2: 0.296 0.896 1.41 0 0.295 0.903 4.72 5.50
## 3: 0.297 0.893 1.41 0 0.296 0.903 4.71 5.63
## 4: 0.298 0.890 1.41 0 0.297 0.902 4.69 5.76
## 5: 0.299 0.888 1.41 0 0.298 0.902 4.68 5.90
## ---
## 668: 0.896 0.296 1.41 0 0.892 0.195 1.56 25.35
## 669: 0.897 0.296 1.41 0 0.893 0.193 1.56 25.35
## 670: 0.898 0.296 1.41 0 0.894 0.191 1.56 25.36
## 671: 0.899 0.295 1.41 0 0.895 0.190 1.56 25.36
## 672: 0.900 0.295 1.41 0 0.896 0.188 1.55 25.37Now, I am creating a data set that will be based on four levels of . I do this by creating a vector . The idea is to create a plot that shows the curve for each value of . The most extreme curve (in this case, the curve all the way to the right, since we are dealing with positive associations only) represents the scenario where (i.e. ). The curves moving to the left reflect increasing sensitivity as increases.
dsenO <- rbindlist(lapply(c(0.0, 0.2, 0.5, 0.8),
function(x) altDGP(dtO, x)))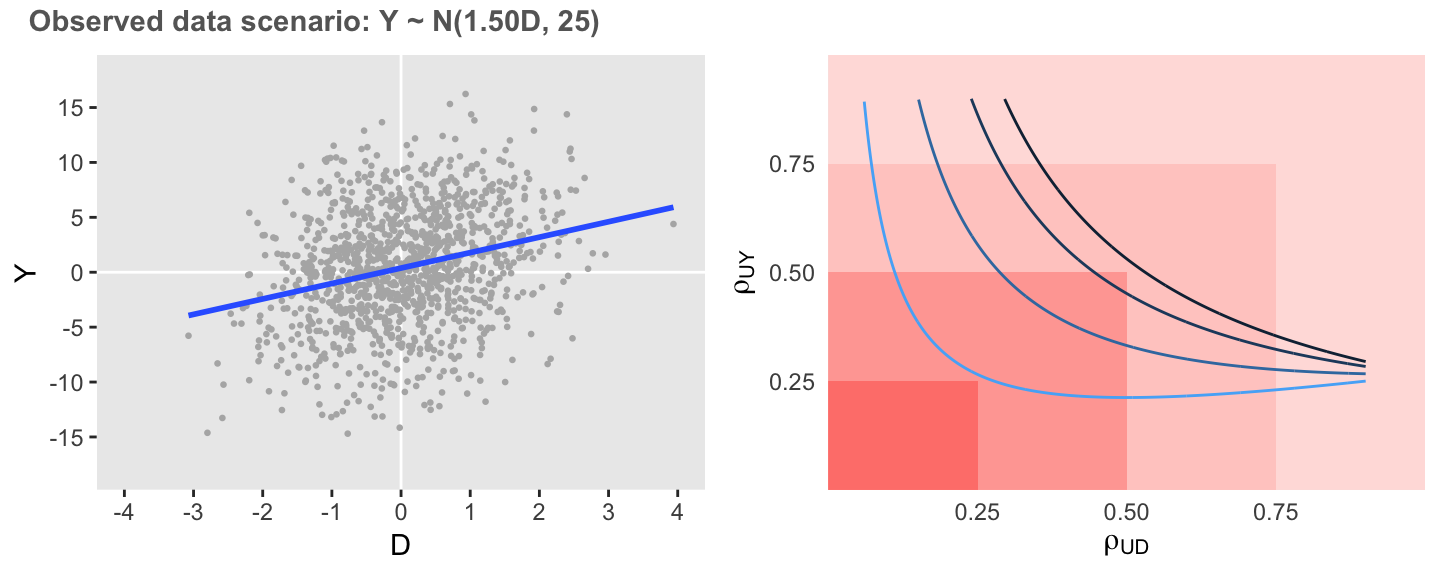
I would say that in this first case the observed association is moderately sensitive to unmeasured confounding, as correlations as low as 0.5 would enough to erase the association.
In the next case, if the association remains unchanged but the variation of is considerably reduced, the observed association is much less sensitive. However, it is still quite possible that the observed overestimation is at least partially overstated, as relatively low levels of correlation could reduce the estimated association.
defA1 <- updateDef(defO, changevar = "Y", newvariance = 4)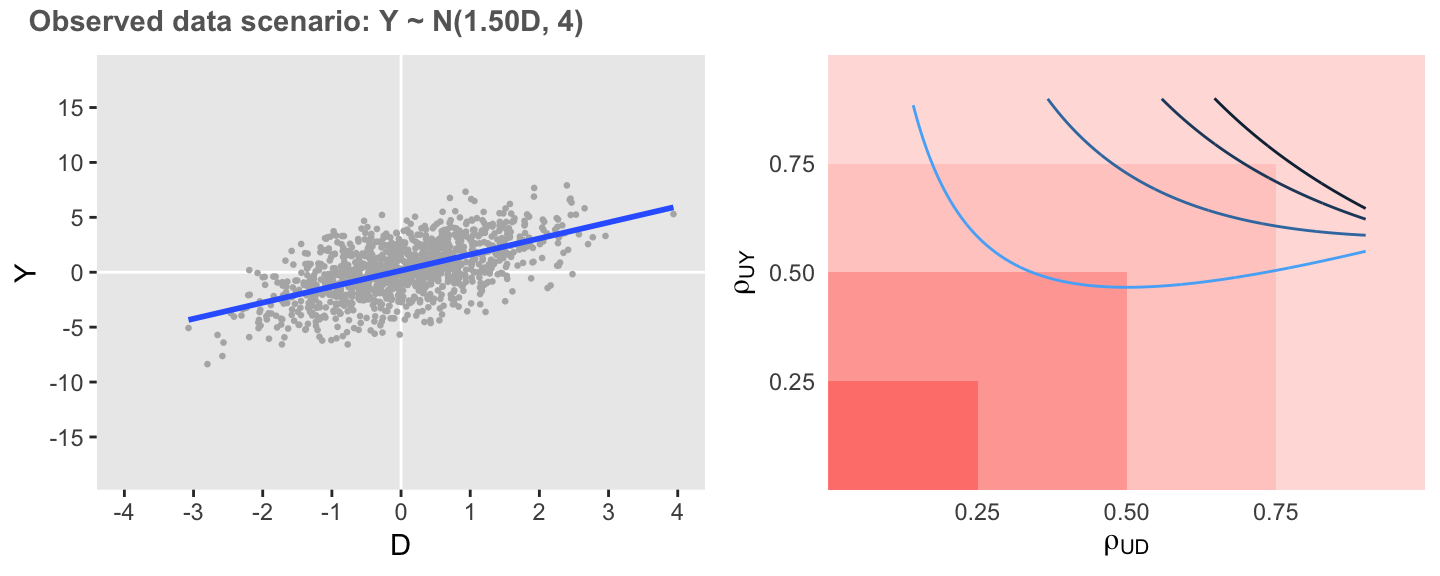
In this last scenario, variance is the same as the initial scenario, but the association is considerably weaker. Here, we see that the estimate of the association is extremely sensitive to unmeasured confounding, as low levels of correlation are required to entirely erase the association.
defA2 <- updateDef(defO, changevar = "Y", newformula = "0.25 * D")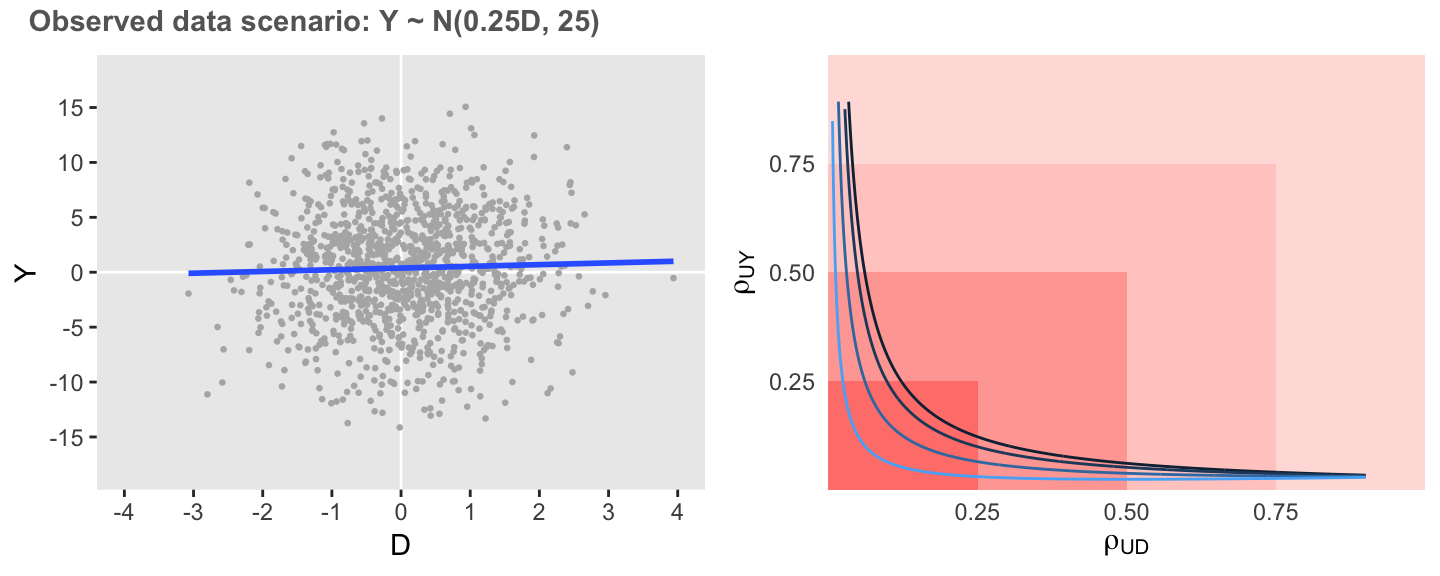
treatSens package
I want to show output generated by the treatSens package I referenced earlier. treatSens requires a formula that includes an outcome vector , an exposure vector , and at least one vector of measured of confounders . In my examples, I have included no measured confounders, so I generate a vector of independent noise that is not related to the outcome.
library(treatSens)
X <- rnorm(1200)
Y <- dtO$Y
Z <- dtO$D
testsens <- treatSens(Y ~ Z + X, nsim = 5)
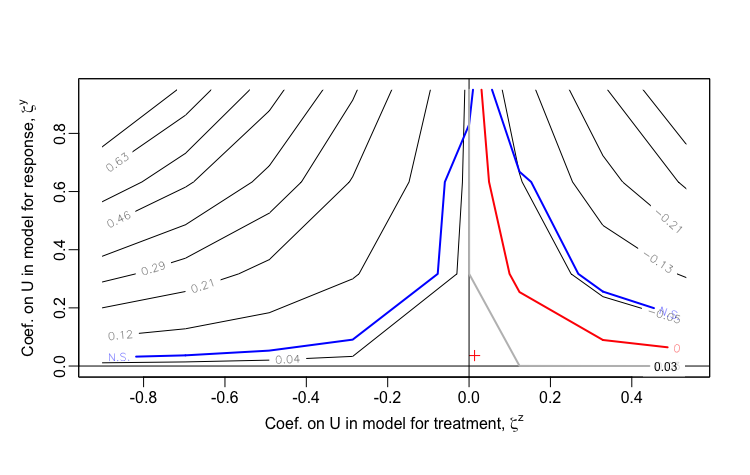
sensPlot(testsens)Once treatSens has been executed, it is possible to generate a sensitivity plot, which looks substantively similar to the ones I have created. The package uses sensitivity parameters and , which represent the coefficients of , the unmeasured confounder. Since treatSens normalizes the data (in the default setting), these coefficients are actually equivalent to the correlations and that are the basis of my sensitivity analysis. A important difference in the output is that treatSens provides uncertainty bands, and extends into regions of negative correlation. (And of course, a more significant difference is that treatSens is flexible enough to handle binary exposures, whereas I have not yet extended my analytic approach in that direction, and I suspect it is no possible for me to do so due to non-collapsibility of logistic regression estimands - I hope to revisit this in the future.)
Observed data scenario 1:
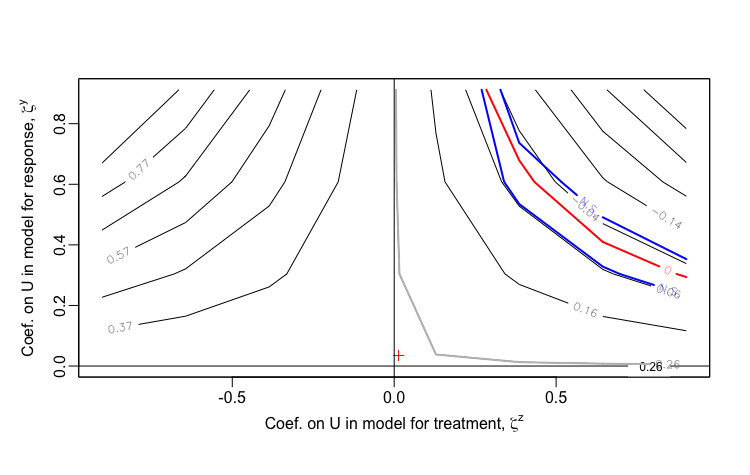
Observed data scenario 2:
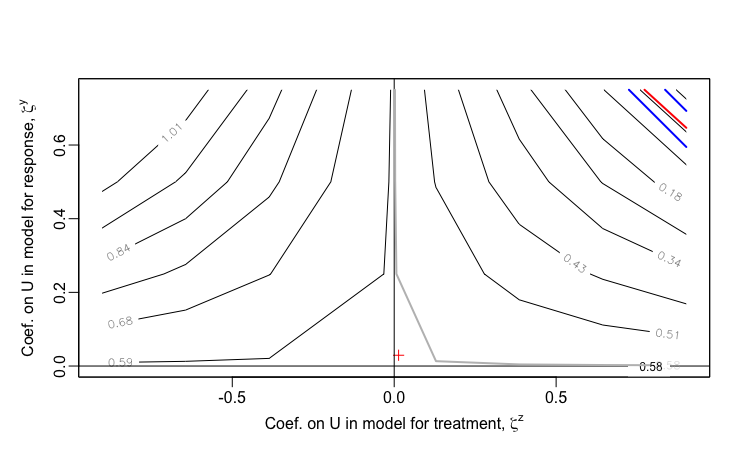
Addendum: Derivation of
In case you want more detail on how we derive from the observed data model and assumed correlation parameters, here it is. We start by specifying the simple observed outcome model:
We can estimate the parameters and using this standard matrix solution:
where is the design matrix:
We can replace with the alternative outcome model:
Note that
Now, we need to figure out what is. First, we rearrange the alternate exposure model:
We can replace :
And now we get back to :
where and come from regressing on :
so,
Since we can center all the observed data, we can easily assume that . All we need to worry about is :
We have generated based on , is a estimated from the data, and is fixed based on some such that . All that remains is :
Since (and )
It follows that
So, now, we have all the elements to generate for a range of ’s and ’s: