Simulation can be super helpful for estimating power or sample size requirements when the study design is complex. This approach has some advantages over an analytic one (i.e. one based on a formula), particularly the flexibility it affords in setting up the specific assumptions in the planned study, such as time trends, patterns of missingness, or effects of different levels of clustering. A downside is certainly the complexity of writing the code as well as the computation time, which can be a bit painful. My goal here is to show that at least writing the code need not be overwhelming.
Recently, I was helping an investigator plan a stepped wedge cluster randomized trial to study the effects of modifying a physician support system on patient-level diabetes management. While analytic approaches for power calculations do exist in the context of this complex study design, it seemed worth the effort to be explicit about all of the assumptions. So in this case I opted to use simulation. The basic approach is outlined below.
The stepped wedge design
In cluster randomized trials, the unit of randomization is the group rather than the individual. While outcomes might be collected at the individual (e.g. student or patient) level, the intervention effect is assessed at the group (e.g. school or clinic). In a stepped wedge cluster design, the randomization unit is still the group, but all groups are eventually exposed to the intervention at some point in the study. Randomization determines when the intervention starts.
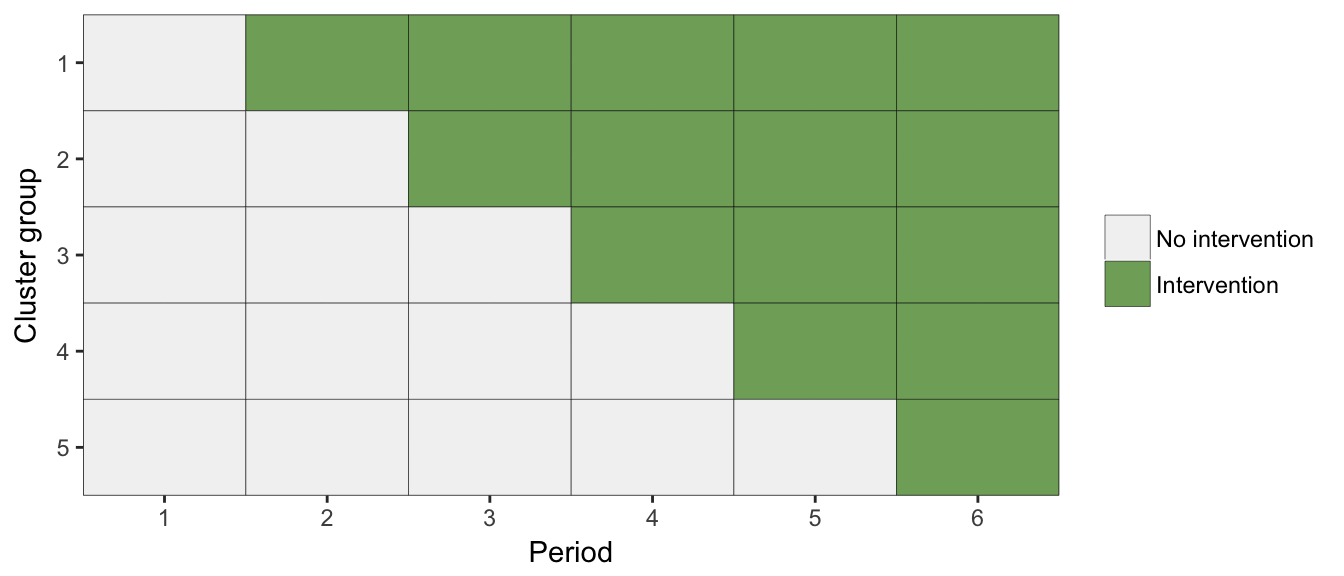
Below is schematic view of how a stepped wedge study is implemented. In this example, a block of clusters receives the intervention starting in the second period, another block starts the intervention in the third period, and so on. The intervention effect is essentially assessed by making within group comparisons. By staggering the starting points, the study is able to distinguish between time effects and treatment effects. If all groups started intervention at the same point, we would need to make an assumption that any improvements were due only to the intervention rather than changes that were occurring over time. This is not an assumption any one can easily justify.
Power and simulation
The statistical power of a study is the conditional probability (conditional on a given effect size), that a hypothesis test will correctly reject the null hypothesis (i.e. conclude there is an effect when there actually is one). Power is underscored by the notion that a particular study can be replicated exactly over and over again. So, if the power of a study is 80%, that means in 80% of the replications of that study we will (appropriately) reject the null hypothesis.
So, to estimate power, we can simulate replications of the study many times and conduct repeated hypothesis tests. The proportion of tests where we reject the null hypothesis is the estimated power. Each of these replications is based on the same set of data generating assumptions: effect sizes, sample sizes, individual level variation, group level variation, etc.
Simulating from a stepped wedge design
In this example, we are assuming a 3-year study with four groups of clusters randomized to start an intervention at either 12 months, 18 months, 24 months, or 30 months (i.e. every 6 months following the 1st baseline year). The study would enroll patients at baseline in each of the clusters, and a measurement of a binary outcome (say diabetes under control, or not) would be collected at that time. Those patients would be followed over time and the same measurement would be collected every 6 months, concluding with the 7th measurement in the 36th month of the study. (It is totally possible to enroll new patients as the study progresses and have a different follow-up scheme, but this approximates the actual study I was working on.)
The data are generated based on a mixed effects model where there are group level effects (\(b_j\) in the model) as well as individual level effects (\(b_i\)). The model also assumes a very slight time trend before the intervention (e.g. diabetes control is improving slightly over time for an individual), an intervention effect, and an almost non-existent change in the time trend after the intervention. The outcome in each period is generated based on this formula:
\(logit(Y_{ijt}) = 0.8 + .01 * period + 0.8 * I_{jt} + 0.001 * I_{jt} * (period-s_j) + b_i + b_j,\)
where \(period\) goes from 0 to 6 (period 0 is the baseline, period 1 is the 6 month follow, etc.), \(I_{jt}\) is 1 if cluster \(j\) is in the intervention in period \(t\), \(s_j\) is the period where the intervention starts for cluster \(j\), and \(logit(Y_{ijt})\) is the log odds of the outcome \(Y\) for individual \(i\) in cluster \(j\) during period \(t\).
We start by defining the data structure using simstudy “data def”" commands. We are assuming that there will be 100 individuals followed at each site for the full study. (We are not assuming any dropout, though we could easily do that.) In this particular case, we are assuming an effect size of 0.8 (which is a log odds ratio):
library(simstudy)
starts <- "rep(c(2 : 5), each = 10)"
siteDef <- defData(varname = "bj", dist = "normal", formula = 0,
variance = .01, id="site")
siteDef <- defData(siteDef, varname = "sj", dist = "nonrandom",
formula = starts)
siteDef <- defData(siteDef, varname = "ips", dist = "nonrandom",
formula = 100)
indDef <- defDataAdd(varname = "bi", dist = "normal", formula = 0,
variance = 0.01)
trtDef <- defDataAdd(varname = "Ijt" ,
formula = "as.numeric(period >= sj)",
dist = "nonrandom")
f = "0.8 + .01 * period + 0.8 * Ijt + 0.001 * Ijt * (period-sj) + bi + bj"
trtDef <- defDataAdd(trtDef, varname = "Yijt", formula = f,
dist = "binary", link = "logit")To generate 40 clusters of data, we use the following code:
set.seed(6789)
dtSite <- genData(40, siteDef)
dtSite <- genCluster(dtSite, cLevelVar = "site", numIndsVar = "ips",
level1ID = "id")
dtSite <- addColumns(indDef, dtSite)
dtSiteTm <- addPeriods(dtSite, nPeriods = 7, idvars = "id")
dtSiteTm <- addColumns(trtDef, dtSiteTm)
dtSiteTm## id period site bj sj ips bi timeID Ijt Yijt
## 1: 1 0 1 -0.1029785 2 100 0.08926153 1 0 1
## 2: 1 1 1 -0.1029785 2 100 0.08926153 2 0 1
## 3: 1 2 1 -0.1029785 2 100 0.08926153 3 1 1
## 4: 1 3 1 -0.1029785 2 100 0.08926153 4 1 1
## 5: 1 4 1 -0.1029785 2 100 0.08926153 5 1 1
## ---
## 27996: 4000 2 40 0.1000898 5 100 0.18869371 27996 0 1
## 27997: 4000 3 40 0.1000898 5 100 0.18869371 27997 0 0
## 27998: 4000 4 40 0.1000898 5 100 0.18869371 27998 0 1
## 27999: 4000 5 40 0.1000898 5 100 0.18869371 27999 1 1
## 28000: 4000 6 40 0.1000898 5 100 0.18869371 28000 1 1And to visualize what the study data might looks like under these assumptions:
# summary by site
dt <- dtSiteTm[, .(Y = mean(Yijt)), keyby = .(site, period, Ijt, sj)]
ggplot(data = dt, aes(x=period, y=Y, group=site)) +
geom_hline(yintercept = c(.7, .83), color = "grey99") +
geom_line(aes(color=factor(site))) +
geom_point(data = dt[sj == period], color="grey50") +
theme(panel.background = element_rect(fill = "grey90"),
panel.grid = element_blank(),
plot.title = element_text(size = 10, hjust = 0),
panel.border = element_rect(fill = NA, colour = "gray90"),
legend.position = "none",
axis.title.x = element_blank()
) +
ylab("Proportion controlled") +
scale_x_continuous(breaks = seq(0, 10, by = 2),
labels = c("Baseline", paste("Year", c(1:5)))) +
scale_y_continuous(limits = c(.5, 1),
breaks = c(.5, .6, .7, .8, .9, 1)) +
ggtitle("Stepped-wedge design with immediate effect") +
facet_grid(sj~.)
Estimating power
We are going to estimate power using only 20 clusters and effect size of 0.25. (Assuming 40 clusters and a large effect size was useful for visualizing the data, but not so interesting for illustrating power, since under those assumptions we are virtually guaranteed to find an effect.)
After generating the data (code not shown) for one iteration, we fit a generalized mixed effects model to show the effect estimate. In this case, the effect estimate is 1.46 (95% CI 1.21-1.77) on the odds ratio scale or 0.37 (95% CI 0.19-0.57) on the log odds ratio scale.
library(lme4)
library(sjPlot)
glmfit <- glmer(data = dtSiteTm,
Yijt ~ period + Ijt + I(Ijt*(period - sj)) + (1|id) + (1|site),
family="binomial" )
sjt.glmer(glmfit, show.icc = FALSE, show.dev = FALSE)| Yijt | ||||
| Odds Ratio | CI | p | ||
| Fixed Parts | ||||
| (Intercept) | 2.15 | 1.90 – 2.44 | <.001 | |
| period | 1.00 | 0.95 – 1.06 | .959 | |
| Ijt | 1.46 | 1.21 – 1.77 | <.001 | |
| I(Ijt * (period - sj)) | 0.99 | 0.91 – 1.07 | .759 | |
| Random Parts | ||||
| τ00, id | 0.011 | |||
| τ00, site | 0.029 | |||
| Nid | 1000 | |||
| Nsite | 20 | |||
| Observations | 7000 | |||
In order to estimate power, we need to generate a large number of replications. I created a simple function that generates a new data set every iteration based on the definitions. If we want to vary the model assumptions across different replications, we can write code to modify the data definition part of the process. In this way we could look at power across different sample size, effect size, or variance assumptions. Here, I am only considering a single set of assumptions.
gData <- function() {
dtSite <- genData(nsites, siteDef)
dtSite <- genCluster(dtSite, cLevelVar = "site",
numIndsVar = "ips", level1ID = "id")
dtSite <- addColumns(indDef, dtSite)
dtSiteTm <- addPeriods(dtSite, nPeriods = 7, idvars = "id")
dtSiteTm <- addColumns(trtDef, dtSiteTm)
return(dtSiteTm)
}And finally, we iterate through a series of replications, keeping track of each hypothesis test in the variable result. Typically, it would be nice to replicate a large number of times (say 1000), but this can sometimes take a long time. In this case, each call to glmer is very resource intensive - unfortunately, I know of know way to speed this up (please get in touch if you have thoughts on this) - so for the purposes of illustration, I’ve only used 99 iterations. Note also that I check to see if the model converges in each iteration, and only include results from valid estimates. This can be an issue with mixed effects models, particularly when sample sizes are small. To estimate the power (which in this case is 78%), calculate the proportion of successful iterations with a p-value smaller than 0.05, the alpha-level threshold we have used in our hypothesis test:
result <- NULL
i=1
while (i < 100) {
dtSite <- gData()
glmfit <- tryCatch(glmer(data = dtSite,
Yijt ~ period + Ijt + I(Ijt*(period - sj)) + (1|id) + (1|site),
family="binomial" ),
warning = function(w) { "warning" }
)
if (! is.character(glmfit)) {
pvalue <- coef(summary(glmfit))["Ijt", "Pr(>|z|)"]
result <- c(result, pvalue)
i <- i + 1
}
}
mean(result < .05)## [1] 0.7812To explore the sensitivity of the power estimates to changing underlying assumptions of effect size, sample size, variation, and time trends, we could vary those parameters and run a sequence of iterations. The code gets a little more complicated (essentially we need to change the “data defs” for each set of iterations), but it is still quite manageable. Of course, you might want to plan for fairly long execution times, particularly if you use 500 or 1000 iterations for each scenario, rather than the 100 I used here.