A reader recently inquired about functions in simstudy that could generate data for a balanced multi-factorial design. I had to report that nothing really exists. A few weeks later, a colleague of mine asked if I could help estimate the appropriate sample size for a study that plans to use a multi-factorial design to choose among a set of interventions to improve rates of smoking cessation. In the course of exploring this, I realized it would be super helpful if the function suggested by the reader actually existed. So, I created genMultiFac. And since it is now written (though not yet implemented), I thought I’d share some of what I learned (and maybe not yet learned) about this innovative study design.
Generating multi-factorial data
First, a bit about multi-factorial data. A single factor is a categorical variable that can have any number of levels. In this context, the factor is usually describing some level of intervention or exposure. As an example, if we want to expose some material to one of three temperature settings, the variable would take on the values “cold”, “moderate”, or “hot”.
In the case of multiple factors, we would have, yes, more than one factor. If we wanted to expose the material to different temperatures as well as varying wind conditions, we would have two factors to contend with. We could characterize the wind level as “low” or “high”. In a multi-factorial experiment, we would expose different pieces of the same material to all possible combinations of these two factors. Ideally, each combination would be represented the same number of times - in which case we have a balanced experiment. In this simple example, there are \(2 \times 3 = 6\) possible combinations.
The function genMultiFac has not yet been implemented in simstudy, but the next version will include it. (I am including the code in an appendix at the end of this post in case you can’t wait.) To generate a dataset, specify the number of replications, the number number of factors, and the number of levels within each factor:
library(simstudy)
dmf <- genMultiFac(each = 2, nFactors = 2, levels = c(3, 2),
colNames = c("temp", "wind"))
genFactor(dmf, "temp", labels = c("cold", "moderate", "hot"),
replace = TRUE)## id wind ftemp
## 1: 1 1 cold
## 2: 2 1 cold
## 3: 3 1 moderate
## 4: 4 1 moderate
## 5: 5 1 hot
## 6: 6 1 hot
## 7: 7 2 cold
## 8: 8 2 cold
## 9: 9 2 moderate
## 10: 10 2 moderate
## 11: 11 2 hot
## 12: 12 2 hotgenFactor(dmf, "wind", labels = c("low", "high"),
replace = TRUE)## id ftemp fwind
## 1: 1 cold low
## 2: 2 cold low
## 3: 3 moderate low
## 4: 4 moderate low
## 5: 5 hot low
## 6: 6 hot low
## 7: 7 cold high
## 8: 8 cold high
## 9: 9 moderate high
## 10: 10 moderate high
## 11: 11 hot high
## 12: 12 hot highdmf## id ftemp fwind
## 1: 1 cold low
## 2: 2 cold low
## 3: 3 moderate low
## 4: 4 moderate low
## 5: 5 hot low
## 6: 6 hot low
## 7: 7 cold high
## 8: 8 cold high
## 9: 9 moderate high
## 10: 10 moderate high
## 11: 11 hot high
## 12: 12 hot highHere is a second example using four factors with two levels each using dummy style coding. In this case, there are \(2^4=16\) possible combinations (though we are only showing the first eight rows). In general, if there are \(k\) factors each with 2 levels, there will be \(2^k\) possible combinations:
genMultiFac(each = 1, nFactors = 4)[1:8, ]## id Var1 Var2 Var3 Var4
## 1: 1 0 0 0 0
## 2: 2 1 0 0 0
## 3: 3 0 1 0 0
## 4: 4 1 1 0 0
## 5: 5 0 0 1 0
## 6: 6 1 0 1 0
## 7: 7 0 1 1 0
## 8: 8 1 1 1 0The multi-factorial study design
A multi-factorial experiment is an innovative way to efficiently explore the effectiveness of a large number of innovations in a single experiment. There is a vast literature on the topic, much of which has been written by the Penn State Methodology Center. My colleague plans on using this design in the context of a multi phase optimization strategy (MOST), which is described in an excellent new book by Linda Collins.
My colleague is interested in conducting a smallish-scale study of four possible interventions in order to identify the most promising one for a considerably larger follow-up study. He is open to the idea that the best intervention might actually be a combination of two (though probably not three). One way to do this would be to conduct an RCT with 5 groups, one for each intervention plus a control. The RCT has two potential problems: the sample size requirements could be prohibitive since we are essentially doing 4 RCTs, and there would be no way to assess how interventions work together. The second shortcoming could be addressed by explicitly testing certain combinations, but this would only exacerbate the sample size requirements.
The multi-factorial design addresses both of these potential problems. A person (or unit of analysis) is randomized to a combination of factors. So, in the case of 4 factors, an individual would be assigned to 1 of 16 groups. We can assess the effect of a specific intervention by averaging the effect size across different combinations of the other two interventions. This is easy to see with the aid of a simulation - so let’s do that (using 3 interventions to keep it a bit simpler).
# define the outcome
def <- defCondition(condition = "(f1 + f2 + f3) == 0",
formula = 10, variance = 1, dist = "normal")
def <- defCondition(def, condition = "(f1 + f2 + f3) == 1",
formula = 14, variance = 1, dist = "normal")
def <- defCondition(def, condition = "(f1 + f2 + f3) == 2",
formula = 18, variance = 1, dist = "normal")
def <- defCondition(def, condition = "(f1 + f2 + f3) == 3",
formula = 22, variance = 1, dist = "normal")
# generate the data
set.seed(19287623)
dx <- genMultiFac(20, nFactors = 3, coding = "dummy",
colNames = c("f1","f2", "f3"))
dx <- addCondition(def, dx, newvar = "Y")
# take a look at the data
dx## id Y f1 f2 f3
## 1: 1 7.740147 0 0 0
## 2: 2 8.718723 0 0 0
## 3: 3 11.538076 0 0 0
## 4: 4 10.669877 0 0 0
## 5: 5 10.278514 0 0 0
## ---
## 156: 156 22.516949 1 1 1
## 157: 157 20.372538 1 1 1
## 158: 158 22.741737 1 1 1
## 159: 159 20.066335 1 1 1
## 160: 160 21.043386 1 1 1We can estimate the average outcome for each level of Factor 1 within each combination of Factors 2 and 3. When we do this, it is readily apparent the the effect size (comparing \(\bar{Y}_{f1=1}\) and \(\bar{Y}_{f1=0}\) within each combination) is about 4:
dx[f2 == 0 & f3 == 0, round(mean(Y),1), keyby = f1]## f1 V1
## 1: 0 9.7
## 2: 1 14.4dx[f2 == 0 & f3 == 1, round(mean(Y),1), keyby = f1]## f1 V1
## 1: 0 14.1
## 2: 1 18.3dx[f2 == 1 & f3 == 0, round(mean(Y),1), keyby = f1]## f1 V1
## 1: 0 14
## 2: 1 18dx[f2 == 1 & f3 == 1, round(mean(Y),1), keyby = f1]## f1 V1
## 1: 0 17.9
## 2: 1 21.6And if we actually calculate the average across the four combinations, we see that the overall average effect is also 4:
d1 <- dx[f1 == 1, .(avg = mean(Y)), keyby = .(f2, f3)]
d0 <- dx[f1 == 0, .(avg = mean(Y)), keyby = .(f2, f3)]
mean(d1$avg - d0$avg)## [1] 4.131657The same is true for the other two interventions:
d1 <- dx[f2 == 1, .(avg = mean(Y)), keyby = .(f1, f3)]
d0 <- dx[f2 == 0, .(avg = mean(Y)), keyby = .(f1, f3)]
mean(d1$avg - d0$avg)## [1] 3.719557d1 <- dx[f3 == 1, .(avg = mean(Y)), keyby = .(f1, f2)]
d0 <- dx[f3 == 0, .(avg = mean(Y)), keyby = .(f1, f2)]
mean(d1$avg - d0$avg)## [1] 3.933804Of course, these adjusted intervention effects are much easier to estimate using linear regression.
library(broom)
tidy(lm(Y ~ f1 + f2 + f3, data = dx))[1:3]## # A tibble: 4 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 10.1 0.161
## 2 f1 4.13 0.161
## 3 f2 3.72 0.161
## 4 f3 3.93 0.161Compare with an RCT
In the scenario I just simulated, there was no interaction between the various interventions. That is, the treatment effect of Factor 1 does not depend on the exposure to the other two factors. This was the second limitation of using a more standard RCT approach - but I will not address this just yet.
Here, I want to take a look at how sample size requirements can increase pretty dramatically if we take a more straightforward RCT approach. Previously, a sample of 160 individuals in the multi-factorial design resulted in a standard error of the treatment effect estimates close to 0.16. In order to get comparable precision in the RCT design, we would need about 300 total patients:
defRCT <- defDataAdd(varname = "Y", formula = "10 + (trt != 1)*4",
variance = 1, dist = "normal")
dr <- genData(300)
dr <- trtAssign(dr, nTrt = 4, grpName = "trt")
dr <- addColumns(defRCT, dr)
tidy(lm(Y ~ factor(trt), data = dr))[1:3]## # A tibble: 4 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 10.1 0.120
## 2 factor(trt)2 3.64 0.169
## 3 factor(trt)3 3.84 0.169
## 4 factor(trt)4 3.87 0.169Interaction
It may be the case that an intervention is actually more effective in the presence of a second intervention - and this might be useful information to have when developing the ideal approach (which could be combination of more than one). In the following 3-factor scenario, Factors 1 and 2 each have an effect alone, but together the effect is even stronger. Factor 3 has no effect.
dint <- genMultiFac(100, nFactors = 3, coding = "dummy",
colNames = c("f1","f2", "f3"))
defA <- defDataAdd(varname = "Y",
formula = "10 + 5*f1 + 5*f2 + 0*f3 + 5*f1*f2",
variance = 1, dist = "normal")
dint <- addColumns(defA, dint)If we look at a plot of the averages, we can see that the effect of Factor 1 alone without Factor 2 is about 5, regardless of what Factor 3 is. However, the effect of Factor 1 when Factor 2 is implemented as well is 10:
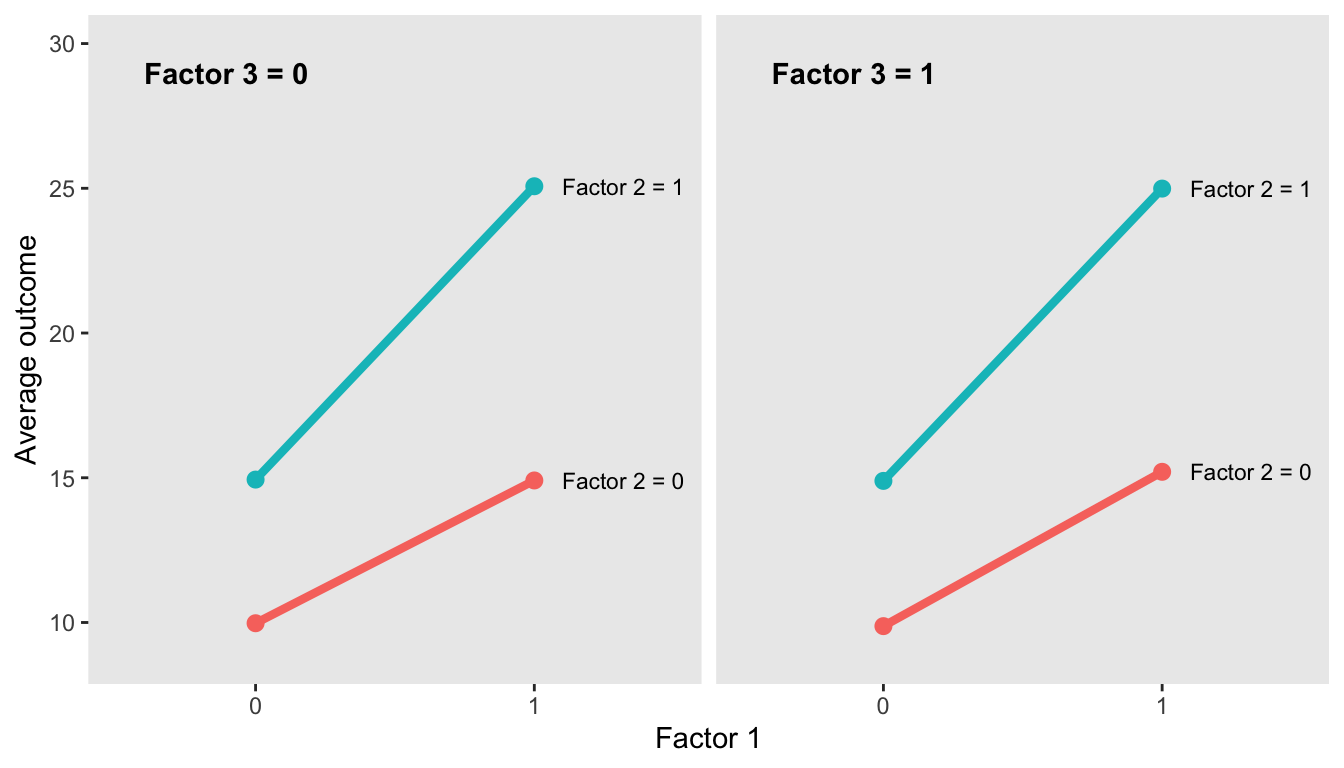
We can fit a linear model with the interaction term and draw the same conclusion. In this case, we might opt for a combination of Factors 1 & 2 to test in a larger study:
tidy(lm(Y ~ f1 * f2 * f3, data = dint))[1:3]## # A tibble: 8 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 9.97 0.103
## 2 f1 4.93 0.145
## 3 f2 4.96 0.145
## 4 f3 -0.100 0.145
## 5 f1:f2 5.20 0.206
## 6 f1:f3 0.399 0.206
## 7 f2:f3 0.0546 0.206
## 8 f1:f2:f3 -0.434 0.291With a more traditional RCT approach, we would never have the opportunity to observe the interaction effect, since by definition each randomization group is limited to a single intervention.
Getting a little technical: effect vs. dummy coding
In the book I mentioned earlier, there is a lengthy discussion about about two different ways to indicate the level of a 2-level factor in the estimation model. What I have been doing so far is what is called “dummy” coding, where the two levels are represented by 0 and 1.
genMultiFac(1, nFactors = 2, coding = "dummy", levels = 2)## id Var1 Var2
## 1: 1 0 0
## 2: 2 1 0
## 3: 3 0 1
## 4: 4 1 1An alternative way to code the levels, called “effect” coding in the literature, is to use -1 and +1 instead:
genMultiFac(1, nFactors = 2, coding = "effect", levels = 2)## id Var1 Var2
## 1: 1 -1 -1
## 2: 2 1 -1
## 3: 3 -1 1
## 4: 4 1 1There is not necessarily an ideal approach to take. One of the reasons that effect coding might be preferable is related to the precision of parameter estimates. In a linear regression model, the standard error of the estimated coefficients is proportional to \((X^{\prime}X)^{-1}\), where \(X\) is the design matrix. Let’s simulate a small design matrix based on “dummy” coding:
dx <- genMultiFac(each = 2, nFactors = 2, coding = "dummy",
colNames = (c("f1", "f2")))
dx[, f12 := f1*f2 ]
dm <- as.matrix(dx[, -"id"])
dm <- cbind(rep(1, nrow(dm)), dm)
dm## f1 f2 f12
## [1,] 1 0 0 0
## [2,] 1 0 0 0
## [3,] 1 1 0 0
## [4,] 1 1 0 0
## [5,] 1 0 1 0
## [6,] 1 0 1 0
## [7,] 1 1 1 1
## [8,] 1 1 1 1Here is \((X^{\prime}X)^{-1}\) for the “dummy” model. The covariance matrix of the coefficients is a scalar function of this matrix. It is possible to see that the standard errors of the interaction term will be larger than the standard errors of the main effects term by looking at the diagonal of the matrix. (And looking at the off-diagonal terms, we can see that the coefficient estimates are not independent; that is, they co-vary.)
solve(t(dm) %*% dm)## f1 f2 f12
## 0.5 -0.5 -0.5 0.5
## f1 -0.5 1.0 0.5 -1.0
## f2 -0.5 0.5 1.0 -1.0
## f12 0.5 -1.0 -1.0 2.0And now the same thing with “effect” coding:
dx <- genMultiFac(each = 2, nFactors = 2, coding = "effect",
colNames = (c("f1", "f2")))
dx[, f12 := f1*f2 ]
dm <- as.matrix(dx[, -"id"])
dm <- cbind(rep(1, nrow(dm)), dm)
dm## f1 f2 f12
## [1,] 1 -1 -1 1
## [2,] 1 -1 -1 1
## [3,] 1 1 -1 -1
## [4,] 1 1 -1 -1
## [5,] 1 -1 1 -1
## [6,] 1 -1 1 -1
## [7,] 1 1 1 1
## [8,] 1 1 1 1Below, the values on the diagonal of the “effect” matrix are constant (and equal the reciprocal of the total number of observations), indicating that the standard errors will be constant across all coefficients. (And here, the off-diagonal terms all equal 0, indicating that the coefficient estimates are independent of each other, which may make it easier to interpret the coefficient estimates.)
solve(t(dm) %*% dm)## f1 f2 f12
## 0.125 0.000 0.000 0.000
## f1 0.000 0.125 0.000 0.000
## f2 0.000 0.000 0.125 0.000
## f12 0.000 0.000 0.000 0.125Here is model estimation of the data set dint we generated earlier with interaction. The first results are based on the original “dummy” coding, which we saw earlier:
tidy(lm(Y ~ f1 * f2 * f3, data = dint))[1:3]## # A tibble: 8 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 9.97 0.103
## 2 f1 4.93 0.145
## 3 f2 4.96 0.145
## 4 f3 -0.100 0.145
## 5 f1:f2 5.20 0.206
## 6 f1:f3 0.399 0.206
## 7 f2:f3 0.0546 0.206
## 8 f1:f2:f3 -0.434 0.291And now changing the coding from “dummy” to “effect”, you can see that the standard error estimates are constant across the coefficients. This consistency can be particularly useful in maintaining statistical power when you are interested not just in main effects but interaction effects as well. (That said, it may still be difficult to have a large enough sample to pick up those interaction effects, just because they are typically smaller than main effects.)
dint[f1 == 0, f1 := -1]
dint[f2 == 0, f2 := -1]
dint[f3 == 0, f3 := -1]
tidy(lm(Y ~ f1 * f2 * f3, data = dint))[1:3]## # A tibble: 8 x 3
## term estimate std.error
## <chr> <dbl> <dbl>
## 1 (Intercept) 16.2 0.0363
## 2 f1 3.81 0.0363
## 3 f2 3.74 0.0363
## 4 f3 0.00903 0.0363
## 5 f1:f2 1.25 0.0363
## 6 f1:f3 0.0454 0.0363
## 7 f2:f3 -0.0406 0.0363
## 8 f1:f2:f3 -0.0543 0.0363How many people do you need?
I started looking into these issues when my colleague asked me to estimate how many people he would need to enroll in his study. I won’t go into it here - maybe in a post soon to come - but I was running into a key challenge. The outcome that we are proposing is not continuous, but binary. Did the patient stop smoking or not? And given that it is really hard to get people to stop smoking, we would likely run into ceiling effects. If one intervention increases the proportion of people abstaining from 10% to 15%, two might be able move that another 2% points. And we might max out with 20% abstention rates for all four interventions applied simultaneously.
The implication of these assumptions (what I would call strong ceiling effects) is that there is pretty severe interaction. Not just two-way interaction, but three- and four-way as well. And logistic regression is notorious for having extremely low power when higher order interactions are involved. I am not sure there is a way around this problem, but I am open to suggestions.
Appendix: genMultiFac code
I’ll leave you with the code to generate multi-factorial data:
genMultiFac <- function(each, nFactors = 2, coding = "dummy", levels = 2,
colNames = NULL, idName = "id") {
if (nFactors < 2) stop("Must specify at least 2 factors")
if (length(levels) > 1 & (length(levels) != nFactors))
stop("Number of levels does not match factors")
x <- list()
if ( all(levels==2) ) {
if (coding == "effect") {
opts <- c(-1, 1)
} else if (coding == "dummy") {
opts <- c(0, 1)
} else {
stop("Need to specify 'effect' or 'dummy' coding")
}
for (i in 1:nFactors) {
x[[i]] <- opts
}
} else {
if (length(levels) == 1) levels <- rep(levels, nFactors)
for (i in 1:nFactors) x[[i]] <- c(1 : levels[i])
}
dt <- data.table(as.data.frame(
lapply(expand.grid(x), function(x) rep(x, each = each)))
)
if (!is.null(colNames)) setnames(dt, colNames)
origNames <- copy(names(dt))
dt[ , (idName) := 1:.N]
setcolorder(dt, c(idName, origNames) )
setkeyv(dt, idName)
return(dt[])
}