I’m contemplating the idea of teaching a course on simulation next fall, so I have been exploring various topics that I might include. (If anyone has great ideas either because you have taught such a course or taken one, definitely drop me a note.) Monte Carlo (MC) simulation is an obvious one. I like the idea of talking about importance sampling, because it sheds light on the idea that not all MC simulations are created equally. I thought I’d do a brief post to share some code I put together that demonstrates MC simulation generally, and shows how importance sampling can be an improvement.
Like many of the topics I’ve written about, this is a vast one that certainly warrants much, much more than a blog entry. MC simulation in particular, since it is so fundamental to the practice of statistics. MC methods are an essential tool to understand the behavior of statistical models. In fact, I’ve probably used MC simulations in just about all of my posts - to generate repeated samples from a model to explore bias, variance, and other distributional characteristics of a particular method.
For example, if we want to assess the variability of a regression parameter estimate, we can repeatedly generate data from a particular “hidden” model, and for each data set fit a regression model to estimate the parameter in question. For each iteration, we will arrive at a different estimate; the variation of all these estimates might be of great interest. In particular, the standard deviation of these estimates is the standard error of the estimate. (Of course, with certain problems, there are ways to analytically derive the standard errors. In these cases, MC simulation can be used to verify an analysis was correct. That’s the beauty of statistics - you can actually show yourself you’ve gotten the right answer.)
A simple problem
In this post, I am considering a simple problem. We are interested in estimating the probability of drawing a value between 2 and 2.5 from a standard normal distribution. That is, we want to use MC simulation to estimate
\[p =P(2.0 <= X <= 2.5), \ \ \ X\sim N(0,1)\]
Of course, we can use R to get us the true \(p\) directly without any simulation at all, but that is no fun:
pnorm(2.5, 0, 1) - pnorm(2, 0, 1)## [1] 0.01654047To do this using simulation, I wrote a simple function that checks to see if a value falls between two numbers.
inSet <- function(x, minx, maxx) {
result <- (x >= minx & x <= maxx)
return(as.integer(result))
}To estimate the desired probability, we just repeatedly draw from the standard normal distribution. After each draw, we check to see if the value falls between 2.0 and 2.5, and store that information in a vector. The vector will have a value of 1 each time a value falls in the range, and 0 otherwise. The proportion of 1’s is the desired probability. Or in other words, \(\hat{p} = \bar{z}\), where \(\bar{z} = \frac{1}{1000} \sum{z}\).
set.seed(1234)
z <- vector("numeric", 1000)
for (i in 1:1000) {
y <- rnorm(1, 0, 1)
z[i] <- inSet(y, 2, 2.5)
}
mean(z)## [1] 0.018The estimate is close to the true value, but there is no reason it would be exact. In fact, I would be suspicious if it were. Now, we can also use the variance of \(z\) to estimate the standard error of \(\hat{p}\):
sd(z)/sqrt(1000)## [1] 0.004206387Faster code?
If you’ve read any of my other posts, you know I am often interested in trying to make R run a little faster. This can be particularly important if we need to repeat tasks over and over, as we will be doing here. The for loop I used here is not ideal. Maybe simstudy (and you could do this without simstudy) can do better. Let’s first see if it provides the same estimates:
library(data.table)
library(simstudy)
# define the data
defMC <- defData(varname = "y", formula = 0,
variance = 1, dist = "normal")
defMC <- defData(defMC, varname = "z", formula = "inSet(y, 2, 2.5)",
dist = "nonrandom")
# generate the data - the MC simulation without a loop
set.seed(1234)
dMC <- genData(1000, defMC)
# evaluate mean and standard error
dMC[ , .(mean(z), sd(z)/sqrt(1000))]## V1 V2
## 1: 0.018 0.004206387So, the results are identical - no surprise there. But which approach used fewer computing resources. To find this out, we turn to the microbenchmark package. (I created a function out of the loop above that returns a vector of 1’s and 0’s.)
library(microbenchmark)
mb <- microbenchmark(tradMCsim(1000), genData(1000, defMC))
summary(mb)[, c("expr", "lq", "mean", "uq", "neval")]## expr lq mean uq neval
## 1 tradMCsim(1000) 2.111598 3.045829 3.215135 100
## 2 genData(1000, defMC) 1.561012 2.092073 1.989184 100With 1000 draws, there is actually very little difference between the two approaches. But if we start to increase the number of simulations, the differences become apparent. With 10000 draws, the simstudy approach is more than 7 times faster. The relative improvement continues to increase as the number of draws increases.
mb <- microbenchmark(tradMCsim(10000), genData(10000, defMC))
summary(mb)[, c("expr", "lq", "mean", "uq", "neval")]## expr lq mean uq neval
## 1 tradMCsim(10000) 26.113492 31.167994 34.050238 100
## 2 genData(10000, defMC) 2.617552 3.258709 3.321416 100Estimating variation of \(\hat{p}\)
Now, we can stop using the loop, at least to generate a single set of draws. But, in order to use MC simulation to estimate the variance of \(\hat{p}\), we still need to use a loop. In this case, we will generate 1500 data sets of 1000 draws each, so we will have 1500 estimates of \(\hat{p}\). (It would probably be best to do all of this using Rcpp, where we can loop with impunity.)
iter <- 1500
estMC <- vector("numeric", iter)
for (i in 1:iter) {
dtMC <- genData(1000, defMC)
estMC[i] <- dtMC[, mean(z)]
}
head(estMC)## [1] 0.019 0.015 0.021 0.018 0.016 0.019We can estimate the average of the \(\hat{p}\)’s, which should be close to the true value of \(p \approx 0.0165\). And we can check to see if the standard error of \(\hat{p}\) is close to our earlier estimate of 0.004.
c(mean(estMC), sd(estMC))## [1] 0.016818667 0.004044175Importance sampling
As we were trying to find an estimate for \(p\) using the simulations above, we spent a lot of time drawing values far outside the range of 2 to 2.5. In fact, almost all of the draws were outside that range. You could almost see that most of those draws were providing little if any information. What if we could focus our attention on the area we are interested in - in this case the 2 to 2.5, without sacrificing our ability to make an unbiased estimate? That would be great, wouldn’t it? That is the idea behind importance sampling.
The idea is to draw from a distribution that is (a) easy to draw from and (b) is close to the region of interest. Obviously, if 100% of our draws is from the set/range in question, then we’ve way over-estimated the proportion. So, we need to reweight the draws in such a way that we get an unbiased estimate.
A very small amount of theory
A teeny bit of stats theory here (hope you don’t jump ship). The expected value of a draw falling between 2 and 2.5 is
\[E_x(I_R) = \int_{-\infty}^{\infty}{I_{R}(x)f(x)dx} \ ,\]
where \(I_R(x)=1\) when \(2.0 \le x \le 2.5\), and is 0 otherwise, and \(f(x)\) is the standard normal density. This is the quantity that we were estimating above. Now, let’s say we want to draw closer to the range in question - say using \(Y\sim N(2.25, 1)\). We will certainly get more values around 2 and 2.5. If \(g(y)\) represents this new density, we can write \(E(I_R)\) another way:
\[E_y(I_R) = \int_{-\infty}^{\infty}{I_{R}(y)\frac{f(y)}{g(y)}g(y)dy} \ .\] Notice that the \(g(y)\)’s cancel out and we end up with the same expectation as above, except it is with respect to \(y\). Also, notice that the second equation is also a representation of \(E_y \left( I_{R}(y)\frac{f(y)}{g(y)} \right)\).
I know I am doing a lot of hand waving here, but the point is that
\[E_x(I_R) = E_y \left( I_{R}\frac{f}{g} \right)\]
Again, \(f\) and \(g\) are just the original density of interest - \(N(0,1)\) - and the “important” density - \(N(2.25, 1)\) - respectively. In our modified MC simulation, we draw a \(y_i\) from the \(N(2.25, 1)\), and then we calculate \(f(y_i)\), \(g(y_i)\), and \(I_R(y_i)\), or more precisely, \(z_i = I_{R}(y_i)\frac{f(y_i)}{g(y_i)}\). To get \(\hat{p}\), we average the \(z_i\)’s, as we did before.
Beyond theory
Why go to all of this trouble? Well, it turns out that the \(z_i\)’s will be much less variable if we use importance sampling. And, as a result, the standard error of our estimate can be reduced. This is always a good thing, because it means a reduction in uncertainty.
Maybe a pretty plot will provide a little intuition? Our goal is to estimate the area under the black curve between 2 and 2.5. An importance sample from a \(N(2.25, 1)\) distribution is represented by the green curve. I think, however, it might be easiest to understand the adjustment mechanism by looking at the orange curve, which represents the uniform distribution between 2 and 2.5. The density is \(g(y) = 2\) for all values within the range, and \(g(y) = 0\) outside the range. Each time we generate a \(y_i\) from the \(U(2,2.5)\), the value is guaranteed to be in the target range. As calculated, the average of all the \(z_i\)’s is the ratio of the area below the black line relative to the area below the orange line, but only in the range between 2 and 2.5. (This may not be obvious, but perhaps staring at the plot for a couple of minutes will help.)
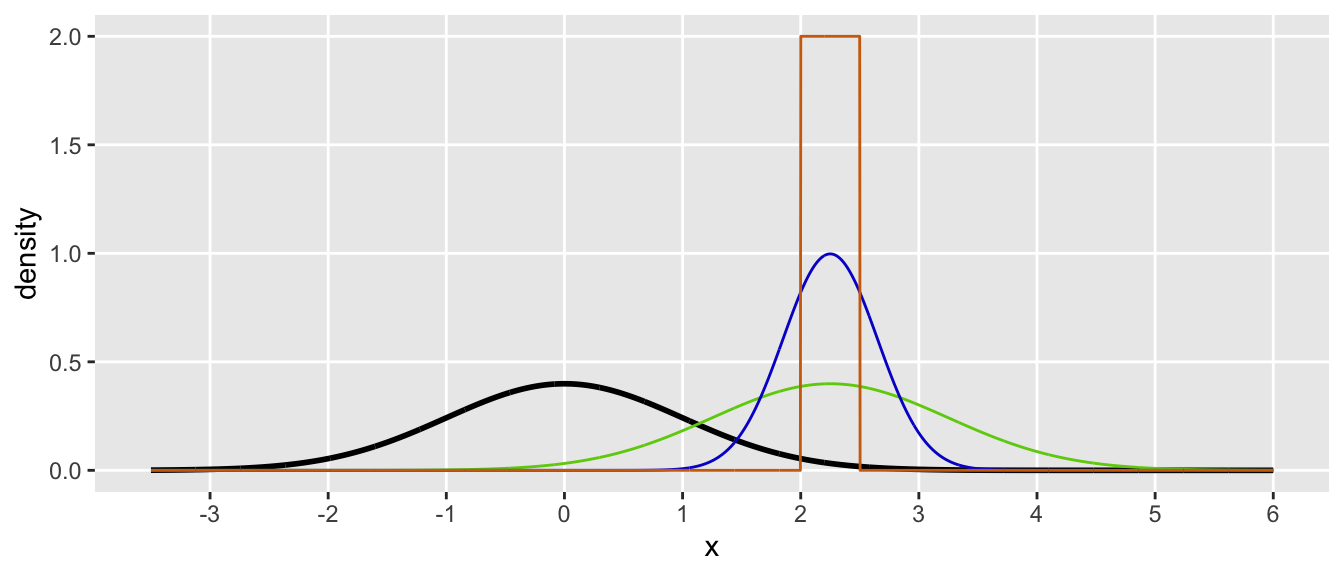
Reducing standard errors by improving focus
Now we can generate data and estimate \(\hat{p}\) and \(se(\hat{p})\). First, here is a simple function to calculate \(z\).
h <- function(I, f, g) {
dx <- data.table(I, f, g)
dx[I != 0, result := I * f / g]
dx[I == 0, result := 0]
return(dx$result)
}We can define the three Monte Carlo simulations based on the three different distributions using simstudy. The elements that differ across the three MC simulations are the distribution we are drawing from and the density \(g\) of that function.
# Normal(2.5, 1)
def1 <- defData(varname = "y", formula = 2.25,
variance = 1, dist = "normal")
def1 <- defData(def1, varname = "f", formula = "dnorm(y, 0, 1)",
dist = "nonrandom")
def1 <- defData(def1, varname = "g", formula = "dnorm(y, 2.25, 1)",
dist = "nonrandom")
def1 <- defData(def1, varname = "I", formula = "inSet(y, 2, 2.5)",
dist = "nonrandom")
def1 <- defData(def1, varname = "z", formula = "h(I, f, g)",
dist = "nonrandom")
# Normal(2.5, .16)
def2 <- updateDef(def1, "y", newvariance = 0.4^2)
def2 <- updateDef(def2, "g", newformula = "dnorm(y, 2.25, 0.4)")
# Uniform(2.0, 2.5)
def3 <- updateDef(def1, "y", newformula = "2.0;2.5",
newvariance = 0, newdist = "uniform")
def3 <- updateDef(def3, "g", newformula = "dunif(y, 2.0, 2.5)")Here is a peek at one data set using the uniform sampling approach:
genData(1000, def3)## id y f g I z
## 1: 1 2.333064 0.02623838 2 1 0.013119192
## 2: 2 2.486934 0.01810877 2 1 0.009054386
## 3: 3 2.232953 0.03297592 2 1 0.016487961
## 4: 4 2.280487 0.02962167 2 1 0.014810835
## 5: 5 2.179042 0.03714037 2 1 0.018570187
## ---
## 996: 996 2.416574 0.02151825 2 1 0.010759125
## 997: 997 2.304301 0.02804796 2 1 0.014023980
## 998: 998 2.113207 0.04277672 2 1 0.021388361
## 999: 999 2.190010 0.03626104 2 1 0.018130520
## 1000: 1000 2.086952 0.04520163 2 1 0.022600813And here are the estimates based on the three different importance samples. Again each iteration is 1000 draws from the distribution - and we use 1500 iterations:
iter <- 1500
N <- 1000
est1 <- vector("numeric", iter)
est2 <- vector("numeric", iter)
est3 <- vector("numeric", iter)
for (i in 1:iter) {
dt1 <- genData(N, def1)
est1[i] <- dt1[, mean(z)]
dt2 <- genData(N, def2)
est2[i] <- dt2[, mean(z)]
dt3 <- genData(N, def3)
est3[i] <- dt3[, mean(z)]
}
# N(2.25, 1)
c(mean(est1), sd(est1))## [1] 0.016534731 0.001123126# N(2.25, .16)
c(mean(est2), sd(est2))## [1] 0.0165235092 0.0006098698# Uniform(2, 2.5)
c(mean(est3), sd(est3))## [1] 0.0165417650 0.0001622635In each case, the average \(\hat{p}\) is 0.0165, and the standard errors are all below the standard MC standard error of 0.0040. The estimates based on draws from the uniform distribution are the most efficient, with a standard error below 0.0002.