Subgroup analysis using a Bayesian hierarchical model

The data

To get this going, here are the libraries used in this post:

library(simstudy)
library(data.table)
library(ggplot2)
library(cmdstanr)
library(posterior)

In this simulated data set of 150 individuals, there are three binary covariates \(A, B, C \in \{0,1\}\) and a treatment indicator \(rx \in \{0,1\}\). When we randomize the individuals to arms, we should have pretty good balance across treatment arms, so a comparison of the two treatment arms without adjusting for the covariates should provide a good estimate of the overall treatment effect. However, we might still be interested in looking at specific subgroups defined by \(A\), \(B\), and \(C\), say patients for whom \(A=0\) or those where \(C=1\). (We could also look at subgroups defined by combinations of these covariates.)

In the data generation process, the treatment effect will be a parameter \(\theta\) that will be determined by the levels of the three covariates. In this case, for patients \(A=B=C=0\), there will be no treatment effect. However, for patients with only \(A=1\) (i.e., \(B=0\) and \(C=0\)), there will be a small treatment effect of \(2\), and there will be a slightly larger effect of \(4\) for patients with \(C=1\), and for patients with \(A=1 \ \& \ C=1\), there will be a treatment effect of \(5\). For patients with \(B=1\) (alone) there is no treatment effect.

d <- defData(varname = "a", formula = 0.6, dist="binary")
d <- defData(d, varname = "b", formula = 0.3, dist="binary")
d <- defData(d, varname = "c", formula = 0.4, dist="binary")
d <- defData(d, varname = "theta", formula = "0 + 2*a  + 4*c - 1*a*c", dist = "nonrandom")

drx <- defDataAdd(varname = "y", formula = "0 + theta*rx", variance = 16, dist = "normal")

In the data generation process, I am assigning eight group identifiers based on the covariates that will be relevant for the Bayes model (described further below).

setgrp <- function(a, b, c) {
  
  if (a==0 & b==0 & c==0) return(1)
  if (a==1 & b==0 & c==0) return(2)
  if (a==0 & b==1 & c==0) return(3)
  if (a==0 & b==0 & c==1) return(4)
  if (a==1 & b==1 & c==0) return(5)
  if (a==1 & b==0 & c==1) return(6)
  if (a==0 & b==1 & c==1) return(7)
  if (a==1 & b==1 & c==1) return(8)
  
}

To generate the data:

set.seed(3871598)

dd <- genData(150, d)
dd <- trtAssign(dd, grpName = "rx")
dd <- addColumns(drx, dd)

dd[, grp:= setgrp(a, b, c), keyby = id]

dd

##       id a b c theta rx     y grp
##   1:   1 1 0 1     5  0  0.28   6
##   2:   2 1 1 0     2  0  3.14   5
##   3:   3 0 0 0     0  0  0.73   1
##   4:   4 1 1 0     2  1  0.78   5
##   5:   5 1 1 1     5  0 -5.94   8
##  ---                             
## 146: 146 1 1 0     2  1  4.68   5
## 147: 147 0 0 1     4  0  3.10   4
## 148: 148 1 0 0     2  0  5.88   2
## 149: 149 1 1 1     5  1  4.22   8
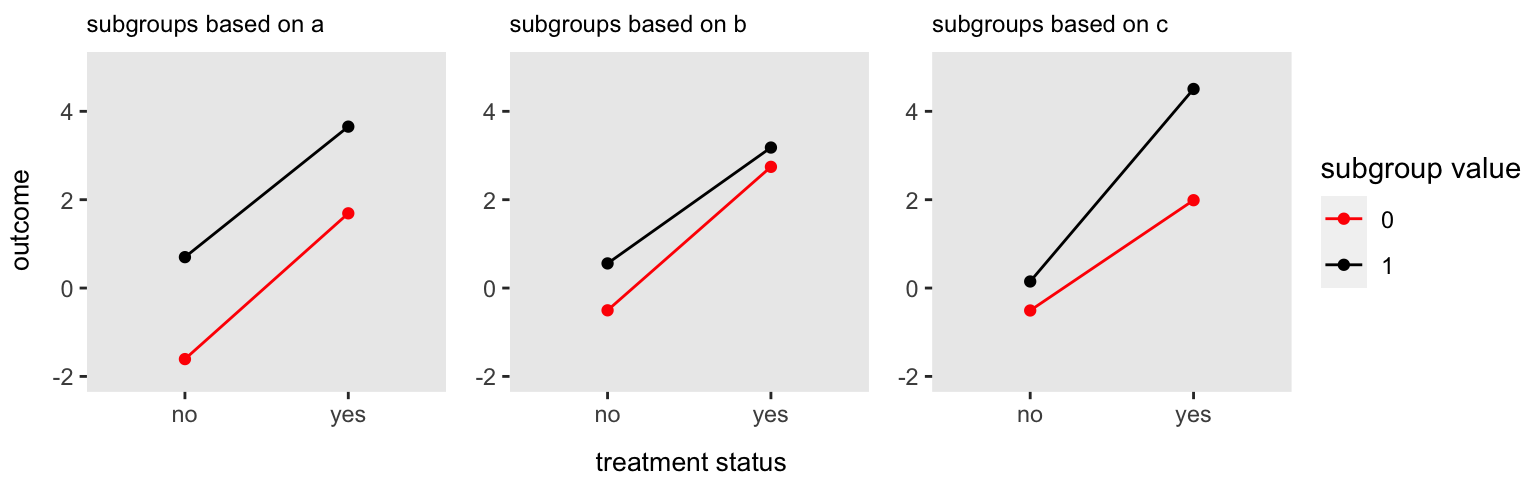
## 150: 150 0 1 1     4  1  4.76   7

Here is a plot of the average outcome \(Y\) for each of the subgroups with and without treatment. The treatment effect for a particular subgroup is the difference of the \(Y\) values for each segment. Now, it appears that there is a treatment effect for the two subgroups \(B=0\) and \(B=1\), yet \(B\) was not supposed to have any impact on the overall effect size, which is \(0\). Just in case this is at all confusing, this is due to the fact that these patients have characteristics \(A\) and \(C\), which do influence the effect size. Indeed, if you compare the subgroups \(B=0\) and \(B=1\), it appears that the effect size could be the same, which is consistent with the fact that \(B\) has no impact on effect size. This is definitely not the case when comparing \(C=0\) and \(C=1\). I point this out, because when I report the estimated effect sizes from the models, I will be reporting the subgroup-specific effects shown here, rather than parameter estimates of \(\theta\).

Subgroup analysis using simple linear regression

Before jumping into the Bayes models, I am fitting seven simple linear regression models to estimate seven treatment effects, one for each of the six subgroups defined by the covariates \(A\), \(B\), and \(C\), plus an overall estimate.

df <- data.frame(dd)

est_lm <- function(dx) {
  fit <- lm(y ~ rx, data = dx)
  c(coef(fit)["rx"], confint(fit)[2,])
}

est_cis <- function(sub_grp) {
  mean_pred <- lapply(split(df[,c(sub_grp, "y", "rx")], df[, c(sub_grp)]), est_lm) 
  do.call(rbind, mean_pred)
}

ci_subgroups <- do.call(rbind, lapply(c("a","b","c"), est_cis))
ci_overall <- est_lm(dd)

cis <- data.table(
  subgroup = c("a = 0", "a = 1", "b = 0", "b = 1", "c = 0", "c = 1", "overall"),
  model = 3,
  rbind(ci_subgroups, ci_overall)
)

setnames(cis, c("rx","2.5 %", "97.5 %"), c("p.50","p.025", "p.975"))

Inspecting the point estimates (denoted as p.50 for the treatment effect for each subgroup (and the overall group), we see that they match pretty closely with the effect sizes depicted in the figure of the means by subgroup above. I’ll compare these estimates to the Bayes estimates in a bit.

cis

##    subgroup model p.50 p.025 p.975
## 1:    a = 0     3  3.3  1.30   5.3
## 2:    a = 1     3  3.0  1.31   4.6
## 3:    b = 0     3  3.2  1.57   4.9
## 4:    b = 1     3  2.6  0.61   4.6
## 5:    c = 0     3  2.5  0.90   4.1
## 6:    c = 1     3  4.4  2.19   6.5
## 7:  overall     3  3.1  1.79   4.4

Two possible Bayesian models

I am including two Bayesian models here, one that I am calling a pooled model and the other an unpooled model (though the second is not absolutely unpooled, just relatively unpooled). In both cases, the outcome model is described as

\[ y_{ij} \sim N\left(\alpha_j +\theta_{j}x_i, \ \sigma_0 \right) \]

where \(y_{ij}\) is the outcome measure for individual \(i\) who has covariate/subgroup pattern \(j\). (These subgroup patterns were defined above in R code. For example group 1 is all cases where \(a=b=c=0\) and group 5 is \(a=b=1, \ c=0\).) \(x_i\) is a treatment indicator, \(x \in \{0,1\}\). \(\alpha_j\) is the intercept for covariate pattern \(j\) (representing the mean outcome for all patients with pattern \(j\) randomized to control). \(\theta_j\) represents the treatment effect for patients with pattern \(j\). \(\sigma_0\) is the within treatment arm/covariate pattern standard deviation, and is assumed to be constant across arms and patterns.

The treatment effect parameter \(\theta_j\) can be further parameterized as function of a set of \(\tau\text{'s}.\) (This parameterization was inspired by this paper by Jones et al.) The treatment effect is a deterministic function of the covariates \(a\), \(b\), and \(c\) as well as their interactions:

So far, the parameterization for the pooled and unpooled models are the same. Now we see how they diverge:

Model estimation

I’m using cmdstanr to estimate the models in Stan. (The Stan code is available if any anyone is interested, or you can try to write it yourself.) For each model, I am sampling in 4 chains of length 2500 following 500 warm-up steps. I’ll skip the required diagnostics here (e.g. trace plots) for brevity, but I did check everything, and things looked OK.

model_pool <- cmdstan_model("code/pooled_subgroup.stan")
model_unpool <- cmdstan_model("code/unpooled_subgroup.stan")

fit_pool <- model_pool$sample(
    data = list(N = dd[,.N], rx = dd[,rx], sub_grp = dd[,grp], y=dd[,y]),
    refresh = 0,
    chains = 4L,
    parallel_chains = 4L,
    iter_warmup = 500,
    iter_sampling = 2500,
    adapt_delta = 0.99,
    max_treedepth = 20,
    seed = 898171
)

## Running MCMC with 4 parallel chains...
## 
## Chain 1 finished in 1.4 seconds.
## Chain 2 finished in 1.4 seconds.
## Chain 3 finished in 1.5 seconds.
## Chain 4 finished in 1.6 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 1.5 seconds.
## Total execution time: 1.8 seconds.

fit_unpool <- model_unpool$sample(
    data = list(N = dd[,.N], rx = dd[,rx], sub_grp = dd[,grp], y=dd[,y], prior_sigma=10),
    refresh = 0,
    chains = 4L,
    parallel_chains = 4L,
    iter_warmup = 500,
    iter_sampling = 2500,
    adapt_delta = 0.99,
    max_treedepth = 20,
    seed = 18717
)

## Running MCMC with 4 parallel chains...
## 
## Chain 3 finished in 1.4 seconds.
## Chain 2 finished in 1.5 seconds.
## Chain 4 finished in 1.7 seconds.
## Chain 1 finished in 2.1 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 1.7 seconds.
## Total execution time: 2.2 seconds.

Extracting posterior probabilities

In this case, I am actually not directly interested in the effect parameters \(\theta_j\), but actually in the estimated treatment effects for the six subgroups defined by \(a=0\), \(a=1\), \(b=0\), \(b=1\), \(c=0\), and \(c=1\). (These groups are not distinct from one another, as each individual has measures for each of \(a\), \(b\), and \(c\).) I will step through the process of how I get these estimates, and then will plot a summary of the estimates.

First, I extract the key parameter estimates into an rvars data structure (I discussed this data structure recently in a couple of posts - here and here). Although the object r below looks like a list of 3 items with just a handful of values, there is actually an entire data set supporting each value that contains 10,000 samples from the posterior distribution. What we are seeing are the mean and standard deviation of those distributions.

r <- as_draws_rvars(fit_pool$draws(variables = c("alpha","theta","sigma")))
r

## # A draws_rvars: 2500 iterations, 4 chains, and 3 variables
## $alpha: rvar<2500,4>[8] mean ± sd:
## [1] -2.42 ± 0.89   0.49 ± 0.79  -1.61 ± 1.46  -0.88 ± 1.09   0.93 ± 1.30 
## [6]  1.06 ± 0.89   2.64 ± 1.59  -0.18 ± 1.19 
## 
## $theta: rvar<2500,4>[8] mean ± sd:
## [1] 2.1 ± 1.03  2.8 ± 0.89  2.7 ± 1.10  3.6 ± 1.11  2.6 ± 1.31  4.2 ± 1.17 
## [7] 4.0 ± 1.31  3.6 ± 1.72 
## 
## $sigma: rvar<2500,4>[1] mean ± sd:
## [1] 3.8 ± 0.23

A cool feature of the rvars data structure (which is part of the package posterior) is that they can be stored in a data.frame, and easily manipulated. Here I am matching the \(\theta_j\) to each individual depending on their covariate pattern \(j\). The plan is to generate simulated data for each individual based on the estimated means and standard deviations.

df <- as.data.frame(dd)
    
df$theta_hat <- r$theta[dd$grp]
df$alpha_hat <- r$alpha[dd$grp]
df$mu_hat <- with(df, alpha_hat + rx* theta_hat)

Here are the first ten rows (out of the 150 individual records):

head(df, 10)

##    id a b c theta rx     y grp  theta_hat    alpha_hat       mu_hat
## 1   1 1 0 1     5  0  0.28   6 4.2 ± 1.17  1.06 ± 0.89  1.06 ± 0.89
## 2   2 1 1 0     2  0  3.14   5 2.6 ± 1.31  0.93 ± 1.30  0.93 ± 1.30
## 3   3 0 0 0     0  0  0.73   1 2.1 ± 1.03 -2.42 ± 0.89 -2.42 ± 0.89
## 4   4 1 1 0     2  1  0.78   5 2.6 ± 1.31  0.93 ± 1.30  3.52 ± 0.96
## 5   5 1 1 1     5  0 -5.94   8 3.6 ± 1.72 -0.18 ± 1.19 -0.18 ± 1.19
## 6   6 1 1 1     5  0 -1.45   8 3.6 ± 1.72 -0.18 ± 1.19 -0.18 ± 1.19
## 7   7 1 1 0     2  0  5.47   5 2.6 ± 1.31  0.93 ± 1.30  0.93 ± 1.30
## 8   8 1 1 0     2  1 -2.33   5 2.6 ± 1.31  0.93 ± 1.30  3.52 ± 0.96
## 9   9 0 0 1     4  1  0.84   4 3.6 ± 1.11 -0.88 ± 1.09  2.69 ± 1.06
## 10 10 1 0 0     2  1  7.05   2 2.8 ± 0.89  0.49 ± 0.79  3.26 ± 0.78

We can add a column of predicted “values” to the data frame.

df$pred <- rvar_rng(rnorm, nrow(df), df$mu_hat, r$sigma)
head(df[,c("id", "grp", "mu_hat", "pred")], 10)

##    id grp       mu_hat        pred
## 1   1   6  1.06 ± 0.89  1.01 ± 3.9
## 2   2   5  0.93 ± 1.30  0.95 ± 4.0
## 3   3   1 -2.42 ± 0.89 -2.41 ± 3.9
## 4   4   5  3.52 ± 0.96  3.53 ± 3.9
## 5   5   8 -0.18 ± 1.19 -0.19 ± 4.0
## 6   6   8 -0.18 ± 1.19 -0.18 ± 4.0
## 7   7   5  0.93 ± 1.30  0.90 ± 4.1
## 8   8   5  3.52 ± 0.96  3.49 ± 3.9
## 9   9   4  2.69 ± 1.06  2.67 ± 3.9
## 10 10   2  3.26 ± 0.78  3.30 ± 3.9

But note that we don’t just have a single value for each of the 150 individuals, but 10,000 samples for each of the 150 individuals (for a total 1.5 million predicted values.) Here is a little bit of evidence that this is the case, as you can see that this is an rvar of dimension \(2500 \text{ samples} \times 4 \text{ chains}\), or \(10,000\) predicted values:

df[9, "pred"]

## rvar<2500,4>[1] mean ± sd:
## [1] 2.7 ± 3.9

Finally, we are ready to get estimates of the within-subgroup effect sizes. I’ve written a little function to help out here. For each covariate \(a\), \(b\), and \(c\), the function splits the data set into four subsets. So, for covariate \(a\) we have \([a=0 \ \& \ rx=0]\), \([a=0 \ \& \ rx=1]\), \([a=1 \ \& \ rx=0]\), and \(a=1 \ \& \ rx=1]\). For each of those subsets, we get a distribution of mean predicted values by averaging across the distribution of individual predicted values. So, the variable effects contains the distribution of effects for the six subgroups (\(a=0\), \(a=1\), \(b=0\), \(b=1\), \(c=0\), and \(c=1\)):

est_effects <- function(sub_grp) {
  mean_pred <- lapply(split(df[,c(sub_grp, "rx","pred")], df[, c(sub_grp, "rx")]), 
    function(x) rvar_mean(x$pred)
  )
  c(mean_pred[["0.1"]] - mean_pred[["0.0"]], mean_pred[["1.1"]] - mean_pred[["1.0"]])
}

effects <- do.call(c, lapply(c("a","b","c"), est_effects))
effects

## rvar<2500,4>[6] mean ± sd:
## [1] 2.5 ± 1.3  3.2 ± 1.1  2.8 ± 1.0  3.1 ± 1.5  2.7 ± 1.1  3.5 ± 1.3

We can also get the distribution of the overall (marginal) treatment effect by sub-setting by \(rx\) only. The last step is to create a summary table for the pooled model. Remember, the effects table is really a table of distributions, and we can extract summary statistics from those distributions for reporting or plotting. Here, we are extracting the \(2.5\%\), \(50\%\), and \(97.5\%\) quantiles to show the median and a \(95\%\) interval.

mean_pred <- lapply(split(df[,c("rx","pred")], df[, "rx"]), function(x) rvar_mean(x$pred))
overall <- mean_pred[["1"]] - mean_pred[["0"]]
    
effects <- c(effects, overall)
    
sumstats_pooled <- data.table( 
  subgroup = c("a = 0", "a = 1", "b = 0", "b = 1", "c = 0", "c = 1", "overall"),
  model = 1,
  p.025 = quantile(effects, 0.025),
  p.50 = quantile(effects, 0.50),
  p.975 = quantile(effects, 0.975)
)

Comparing model estimates

Now to take a look at the distribution of effect sizes based on the different models. (I didn’t show it, but I also created a table called sumstats_unpooled using the same process I just walked you through.) Below is a plot of the effect estimates for each of the subgroups as well as the overall (marginal) effect estimates. The lm plot shows the point estimate with a \(95\%\) confidence interval. The other two plots show the medians of the posterior distributions for the subgroup effects along with \(95\%\) intervals.

Two important things to see in the plot, which will be very important when I write next time about “Type 1” errors, are the relative length of the intervals and the apparent shrinkage of some of the estimates. In all the cases, the length of the interval for the standard linear regression model is smaller than the two Bayesian models, reflecting less uncertainty. The pooled model also appears to have slightly less uncertainty compared to the unpooled model.

The second point is that the point estimates for the linear regression model and the median estimates for the unpooled model are quite close, while the pooled medians appear to be pulled away. The direction of the shrinkage is not coherent, because there is a mixture of main effects and interaction effects (the \(\tau\)’s) that are shifting things around. It appears that the effects of the subgroups \(a=0,\) \(b=0,\) and \(c=0\) are being pulled towards each other, and the same appears to be true for the group defined by \(a=1,\) \(b=1,\) and \(c=1.\) This seems right as we know that the underlying parameters \(\tau_a\), \(\tau_b\), and \(\tau_c\) are shrinking towards each other.

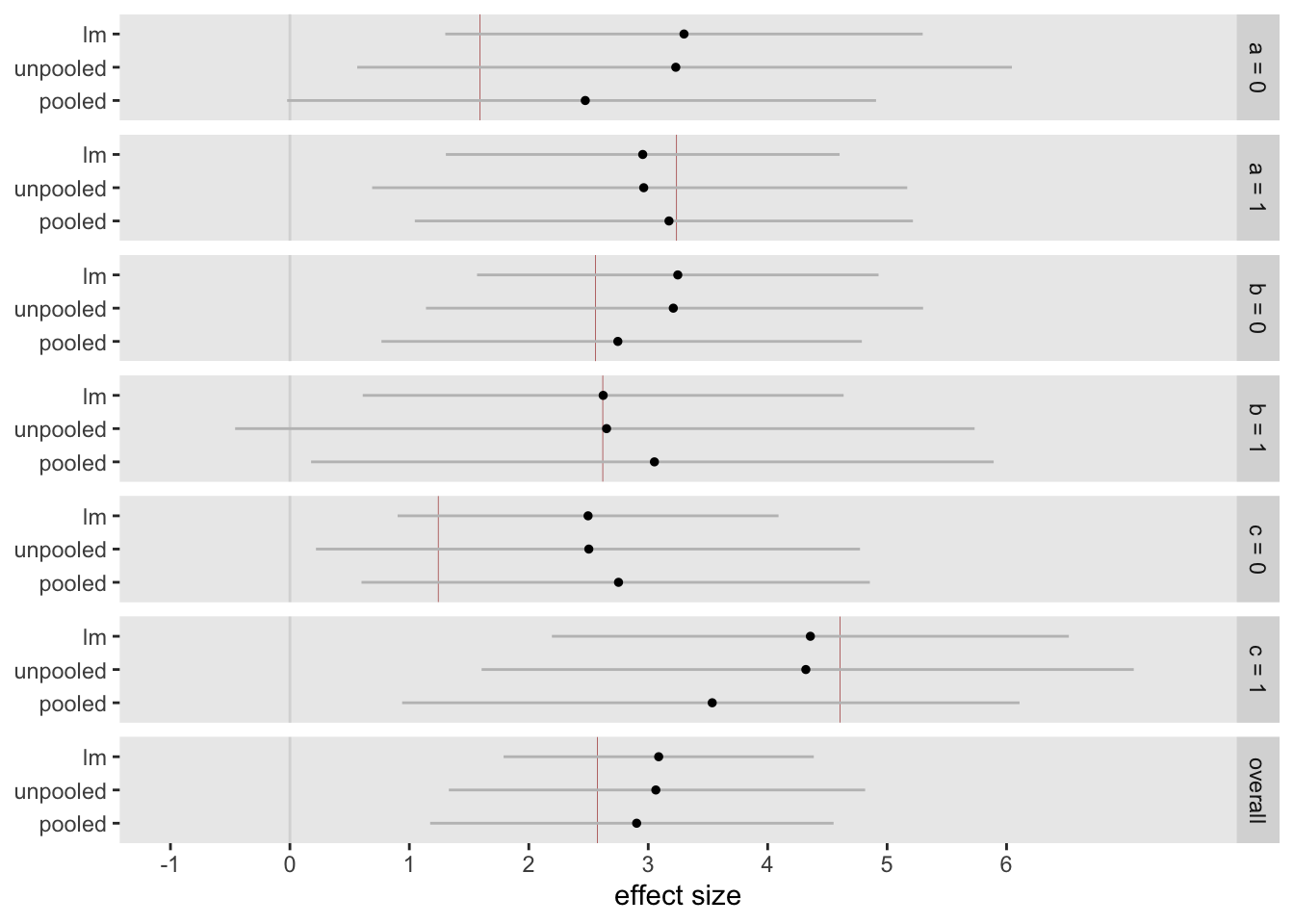
If we were using the pooled model to draw conclusions, I would say that it appears that subgroups defined by \(c\) seem to have heterogeneous treatment effects, though I would probably want to have more data to confirm, as the intervals are still quite wide. If we use the results from the linear regression model, we might want to proceed with caution, because the intervals are likely too narrow, we have not adjusted for multiple testing. We will see this next time when I look at a case where there are no underlying treatment effects in the data generation process.